En el ámbito de la geometría‚ la construcción de rectas paralelas es una habilidad fundamental que se aplica en diversas áreas‚ desde el dibujo técnico hasta la resolución de problemas matemáticos. Este artículo explora el proceso de dibujar una recta paralela a una recta dada y que pasa por un punto determinado‚ utilizando herramientas básicas de geometría como la regla y el compás; Se explicarán los principios geométricos subyacentes a esta construcción‚ así como los pasos necesarios para realizarla con precisión.
Principios Geométricos Fundamentales
La construcción de una recta paralela se basa en los siguientes principios de la geometría euclidiana⁚
- Paralelismo⁚ Dos rectas son paralelas si y solo si no se intersectan en ningún punto. En otras palabras‚ mantienen una distancia constante entre sí a lo largo de toda su extensión.
- Teorema de las rectas paralelas⁚ Si una recta corta a dos rectas paralelas‚ los ángulos correspondientes son iguales‚ los ángulos alternos internos son iguales y los ángulos alternos externos son iguales.
- Construcción con compás y regla⁚ La geometría euclidiana se basa en la construcción de figuras geométricas utilizando únicamente una regla no graduada y un compás. Estas herramientas permiten trazar segmentos de recta‚ arcos de circunferencia y puntos de intersección‚ lo que a su vez facilita la construcción de figuras más complejas.
Pasos para Dibujar una Recta Paralela
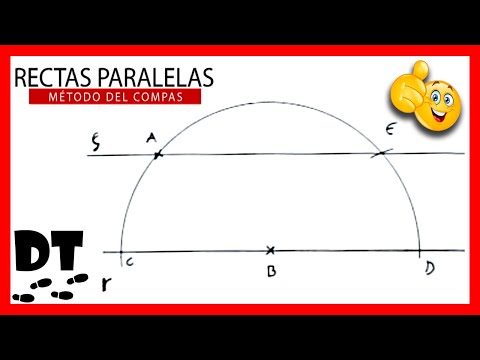
Para dibujar una recta paralela a una recta dada y que pasa por un punto determinado‚ se pueden seguir estos pasos⁚
1. Trazar la Recta Dada y el Punto Determinado
Comienza por trazar la recta dada utilizando una regla. Luego‚ marca el punto determinado fuera de la recta dada. Este punto será el punto por el que pasará la recta paralela.
2. Trazar un Arco de Circunferencia
Con el compás‚ coloca la punta seca en el punto determinado y traza un arco de circunferencia que intersecte la recta dada en dos puntos. Estos puntos de intersección serán cruciales para la construcción de la recta paralela.
3. Trazar un Segundo Arco de Circunferencia
Sin cambiar la abertura del compás‚ coloca la punta seca en uno de los puntos de intersección de la recta dada con el arco de circunferencia. Traza un segundo arco de circunferencia que intersecte al primero. El punto de intersección de estos dos arcos será un punto crucial para la construcción de la recta paralela.
4. Trazar la Recta Paralela
Une el punto determinado con el punto de intersección de los dos arcos de circunferencia utilizando una regla. Esta línea recta será paralela a la recta dada y pasará por el punto determinado.
Explicación Geométrica
La construcción de la recta paralela se basa en el teorema de las rectas paralelas. Los dos arcos de circunferencia trazados en los pasos 2 y 3 garantizan que los ángulos correspondientes formados por la recta dada y la recta paralela sean iguales. Esto se debe a que los arcos de circunferencia tienen la misma abertura‚ lo que significa que los segmentos de recta que conectan los puntos de intersección con el punto determinado tienen la misma longitud. Por lo tanto‚ los ángulos correspondientes son iguales‚ lo que implica que las dos rectas son paralelas.
Aplicaciones Prácticas
La construcción de rectas paralelas tiene numerosas aplicaciones prácticas en diversos campos‚ entre ellos⁚
- Dibujo técnico⁚ En el dibujo técnico‚ las rectas paralelas se utilizan para representar líneas horizontales‚ verticales y oblicuas‚ así como para crear formas geométricas como cuadrados‚ rectángulos y paralelogramos.
- Geometría analítica⁚ En geometría analítica‚ las rectas paralelas se representan mediante ecuaciones de la forma y = mx + b‚ donde m es la pendiente de la recta y b es la ordenada en el origen. Dos rectas son paralelas si y solo si tienen la misma pendiente.
- Arquitectura e ingeniería⁚ En la arquitectura e ingeniería‚ las rectas paralelas se utilizan para diseñar estructuras‚ como puentes‚ edificios y carreteras‚ asegurando la estabilidad y la funcionalidad de las construcciones.
Conclusión
La construcción de una recta paralela a una recta dada y que pasa por un punto determinado es una habilidad fundamental en la geometría. Esta construcción se basa en principios geométricos sólidos y se puede realizar utilizando herramientas básicas como la regla y el compás. Las aplicaciones prácticas de esta construcción son amplias‚ abarcando desde el dibujo técnico hasta la arquitectura y la ingeniería. Al comprender los principios geométricos subyacentes y los pasos necesarios para realizar esta construcción‚ los estudiantes y profesionales pueden aplicar este conocimiento en diversos contextos.

Este artículo proporciona una introducción completa y útil a la construcción de rectas paralelas. La explicación de los principios geométricos es precisa y fácil de entender, y los pasos para la construcción son claros y concisos. La referencia a la geometría euclidiana y la construcción con compás y regla le da al artículo un contexto histórico y práctico.
El artículo presenta una descripción completa y precisa de la construcción de rectas paralelas. La explicación de los principios geométricos fundamentales y los pasos de construcción son claros y fáciles de entender. La referencia a la geometría euclidiana y la construcción con compás y regla le da al artículo un contexto histórico y práctico. Se podría considerar la inclusión de ejemplos adicionales o aplicaciones de la construcción de rectas paralelas en diferentes campos.
Este artículo proporciona una introducción clara y concisa a la construcción de rectas paralelas utilizando herramientas básicas de geometría. La explicación de los principios geométricos subyacentes es precisa y fácil de entender. La presentación paso a paso de la construcción es práctica y útil para los estudiantes que aprenden este concepto por primera vez. Sin embargo, se podría considerar la inclusión de ejemplos visuales o diagramas para ilustrar mejor los pasos involucrados en la construcción.
La información proporcionada en este artículo es precisa y bien organizada. La explicación de los principios geométricos es clara y concisa, y los pasos para la construcción de rectas paralelas están bien descritos. La referencia a la geometría euclidiana y la construcción con compás y regla le da al artículo un contexto histórico y práctico.
Este artículo es una excelente introducción a la construcción de rectas paralelas. La explicación de los principios geométricos es accesible para un público amplio, y los pasos para la construcción son fáciles de seguir. La inclusión de ejemplos visuales o diagramas sería un complemento valioso para el artículo.
El artículo aborda de manera efectiva el tema de la construcción de rectas paralelas, utilizando un lenguaje técnico adecuado y una estructura lógica. La referencia a los principios geométricos fundamentales, como el paralelismo y el teorema de las rectas paralelas, es esencial para comprender el concepto. La inclusión de pasos específicos para la construcción con compás y regla facilita la aplicación práctica del conocimiento.
El artículo ofrece una explicación detallada y bien estructurada sobre la construcción de rectas paralelas. La descripción de los principios geométricos subyacentes es clara y concisa, y los pasos para la construcción son fáciles de seguir. La referencia a la geometría euclidiana y la construcción con compás y regla le da al artículo un contexto histórico y práctico.