Introducción
En geometría, la construcción de figuras geométricas es una habilidad fundamental que permite a los estudiantes comprender las propiedades de las formas y desarrollar su razonamiento espacial. Una construcción común es la de dibujar una perpendicular a un segmento dado a través de un cierto punto que se encuentra en este segmento. Esta construcción tiene numerosas aplicaciones en geometría, trigonometría y otras áreas de las matemáticas.
Este artículo proporcionará una guía paso a paso sobre cómo dibujar una perpendicular a un segmento dado a través de un cierto punto que se encuentra en este segmento, utilizando herramientas básicas de geometría como un compás y una regla. Además, se discutirá la teoría matemática que sustenta esta construcción y se proporcionarán ejemplos para ilustrar el proceso.
Conceptos básicos
Antes de comenzar la construcción, es esencial comprender algunos conceptos básicos de geometría⁚
- Segmento de línea⁚ Una parte de una línea recta que tiene dos puntos finales definidos.
- Punto⁚ Una ubicación específica en el espacio que no tiene dimensión.
- Perpendicular⁚ Dos líneas o segmentos de línea que se cruzan en un ángulo recto (90 grados).
- Ángulo recto⁚ Un ángulo que mide 90 grados.
- Compás⁚ Una herramienta de dibujo que se utiliza para dibujar círculos y arcos.
- Regla⁚ Una herramienta de dibujo que se utiliza para medir longitudes y dibujar líneas rectas.
- Intersección⁚ El punto donde dos o más líneas, segmentos de línea o curvas se cruzan.
- Bisectriz⁚ Una línea o segmento de línea que divide un ángulo o un segmento de línea en dos partes iguales.
Construcción de la perpendicular
Para dibujar una perpendicular a un segmento dado a través de un cierto punto que se encuentra en este segmento, siga estos pasos⁚
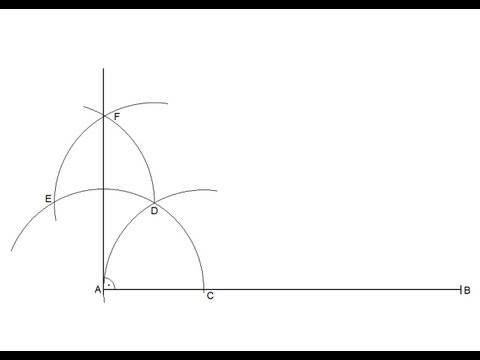
- Paso 1⁚ Dibujar el segmento dado. Etiquete los puntos finales del segmento como A y B.
- Paso 2⁚ Marcar el punto dado en el segmento. Etiquete este punto como C.
- Paso 3⁚ Utilizando el compás, con C como centro, dibujar un arco que interseque el segmento AB en dos puntos. Etiquete estos puntos como D y E.
- Paso 4⁚ Utilizando el compás, con D como centro, dibujar un arco en el lado opuesto del segmento AB.
- Paso 5⁚ Utilizando el compás, con E como centro, dibujar otro arco que interseque el arco anterior. Etiquete el punto de intersección como F.
- Paso 6⁚ Utilizando la regla, dibujar una línea recta que pase por los puntos C y F. Esta línea es perpendicular al segmento AB y pasa por el punto C.
Explicación matemática
La construcción de la perpendicular se basa en el teorema de Pitágoras y la definición de un ángulo recto. El teorema de Pitágoras establece que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados. En la construcción, el triángulo CDE es un triángulo rectángulo, donde CD y CE son los catetos y DE es la hipotenusa.
Al dibujar los arcos con D y E como centros, se asegura que los puntos D y E estén a la misma distancia del punto C. Esto significa que CD y CE tienen la misma longitud. Por lo tanto, el triángulo CDE es un triángulo isósceles.
Debido a que el triángulo CDE es isósceles y tiene un ángulo recto en C, los ángulos D y E son iguales y miden 45 grados cada uno. Por lo tanto, el ángulo FCD es un ángulo recto, lo que significa que la línea CF es perpendicular al segmento AB.
Aplicaciones
La construcción de una perpendicular a un segmento dado a través de un cierto punto que se encuentra en este segmento tiene numerosas aplicaciones en geometría y otras áreas de las matemáticas, incluyendo⁚
- Dividir un segmento de línea en dos partes iguales⁚ La perpendicular a un segmento de línea a través de su punto medio lo divide en dos partes iguales.
- Construir un cuadrado⁚ La perpendicular a un lado de un cuadrado a través de su punto medio se puede utilizar para construir el lado opuesto del cuadrado.
- Construir un triángulo rectángulo⁚ La perpendicular a un lado de un triángulo rectángulo a través de su punto medio se puede utilizar para construir la hipotenusa del triángulo.
- Encontrar la distancia entre un punto y una línea⁚ La perpendicular desde un punto a una línea es la distancia más corta entre el punto y la línea.
Conclusión
La construcción de una perpendicular a un segmento dado a través de un cierto punto que se encuentra en este segmento es una habilidad esencial en geometría. Esta construcción se basa en conceptos básicos de geometría, como el teorema de Pitágoras y la definición de un ángulo recto. La construcción tiene numerosas aplicaciones en geometría y otras áreas de las matemáticas, lo que la convierte en una habilidad valiosa para los estudiantes de todos los niveles.
Al dominar esta construcción, los estudiantes pueden desarrollar su razonamiento espacial y su comprensión de las propiedades de las formas geométricas. Esta habilidad puede ser utilizada para resolver problemas complejos en geometría y otras áreas de las matemáticas.

El artículo presenta una guía práctica y útil para la construcción de una perpendicular a un segmento dado. La estructura del artículo es lógica y fácil de seguir. La inclusión de conceptos básicos relevantes y ejemplos es una práctica excelente para asegurar la comprensión del lector.
La estructura del artículo es organizada y coherente. La sección de conceptos básicos es esencial para la comprensión del lector, y la construcción paso a paso es detallada y precisa. La inclusión de ejemplos y la explicación de la teoría matemática contribuyen a la claridad y profundidad del contenido.
El artículo es un recurso valioso para estudiantes de geometría. La explicación de la construcción es clara y concisa, y los diagramas son fáciles de entender. La inclusión de la teoría matemática que sustenta la construcción es un punto a favor, ya que permite una comprensión más profunda del tema.
El artículo ofrece una excelente introducción a la construcción de una perpendicular a un segmento dado. La terminología utilizada es precisa y el lenguaje es claro y conciso. La inclusión de diagramas y ejemplos facilita la comprensión del proceso. El artículo es un recurso útil para estudiantes que están aprendiendo geometría básica.
El artículo es un recurso valioso para estudiantes y profesores de geometría. La presentación del tema es lógica y fácil de seguir. La utilización de herramientas básicas de geometría, como el compás y la regla, lo hace accesible a un público amplio. La inclusión de la teoría matemática que sustenta la construcción es un punto a favor, ya que permite una comprensión más profunda del tema.
El artículo es informativo y bien escrito. La explicación paso a paso de la construcción es fácil de seguir, y los diagramas son claros y útiles. La sección de conceptos básicos es una buena introducción al tema, y la inclusión de ejemplos es útil para la comprensión del lector.
El artículo es un recurso excelente para estudiantes que están aprendiendo geometría. La explicación paso a paso de la construcción es fácil de seguir, y los diagramas son claros y útiles. La inclusión de ejemplos y la explicación de la teoría matemática contribuyen a la claridad y profundidad del contenido.
Este artículo presenta una guía clara y concisa sobre la construcción de una perpendicular a un segmento dado. La explicación paso a paso, junto con los diagramas, facilita la comprensión del proceso. La inclusión de conceptos básicos relevantes antes de la construcción es una práctica excelente, ya que asegura que el lector tenga las bases necesarias. La sección de ejemplos es útil para reforzar la comprensión del lector y aplicar los conocimientos adquiridos.